Die Progress Unit (DPU) is the amount of time you’d have to go ahead to be shocked enough at the world to die
The DPU is a colorful illustration of an idea from futurist Ray Kurzweil, the author of The Singularity is Near: the law-of-accelerating-returns.
Urban’s big idea here is that human progress is exponential. In the present moment, though, it’s hard to recognize or comprehend that the graph is about to go vertical.

This is demonstrably true, using DPUs or actual numbers, but according to Urban, there are three reasons we can’t grok the impact of exponential progress:
-
When it comes to history, we think in straight lines. It’s really hard to grasp how much crazier the future is going to get, because most people extrapolate based on the past growth rate, and even the more optimistic and adventurous ones will extrapolate from the present growth rate. If you accept that the rate of progress is accelerating, then it follows that using past or even present rates undershoots.
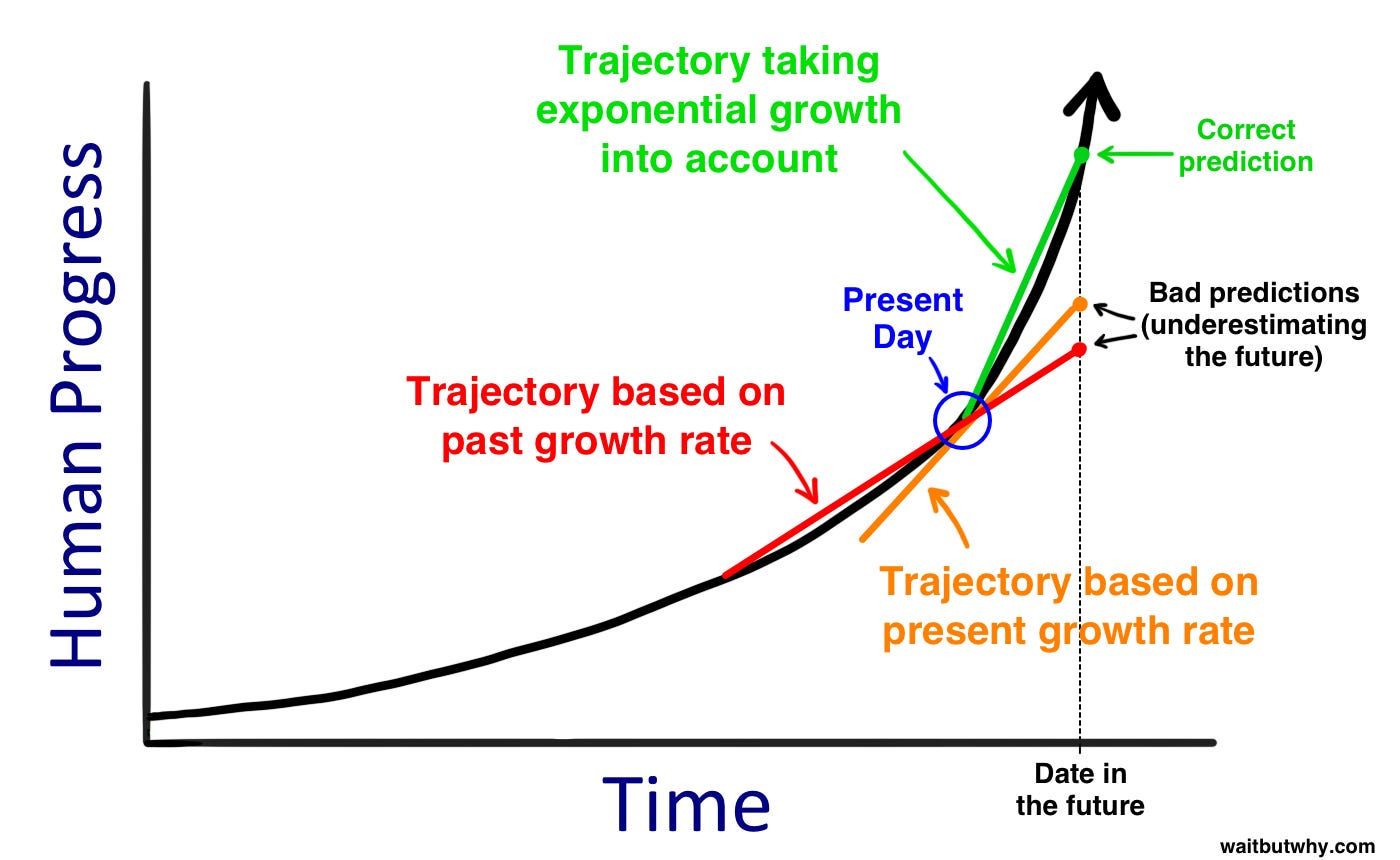
-
The trajectory of very recent history often tells a distorted story. Making this even harder, in the short-term, assuming an accelerating growth rate might make you look silly or lose money. The progression isn’t smooth. A period of rapid growth might give way to a period of slower growth. Progress happens in S-Curves -- similar to the Gartner Hype Cycle that we so often talk about here -- and it might even look like we’re regressing in certain areas at points. But over time, if you zoom out, those are just squiggles on an exponential curve arcing up and to the right.
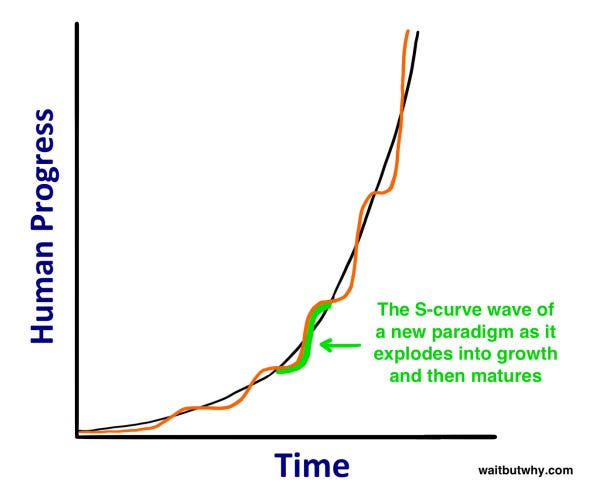
-
**Our own experience makes us stubborn old men about the future.**We have lived through past growth rates. We’ve never lived through future growth. Therefore, it’s a lot easier for us to intuit what the future will be like by extrapolating linearly based on what we’ve actually experienced. Yes, things will be different, we all know that, but they’ll be different in predictable ways. We expect that anything that deviates too far from our past experience, or historical averages, will revert to the mean.
