Moore machine

What is a Moore machine?

A Moore machine is a finite-state-automata where the output values are determined by only its current state. Moore machines are a restricted type of a finite-state-transducer.

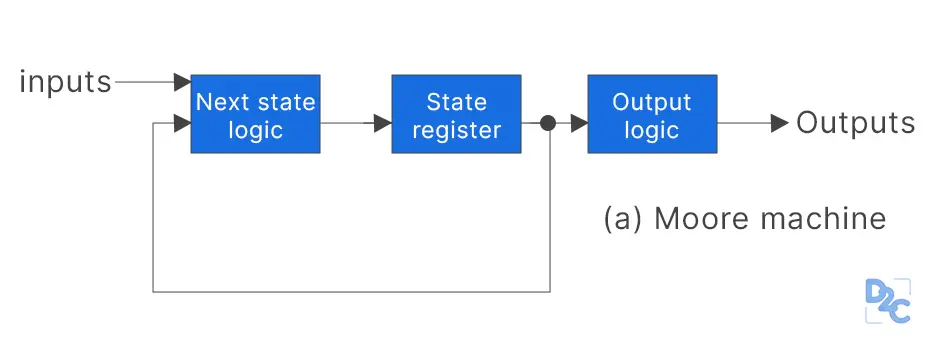
Mathematical model

As per the general classification noted on UC Davis outline on transducers (formatted with similar variables to [[Finite-state automata]]s), a deterministic Moore machine has 6 main variables associated with its definition (a sextuple): ( $\Sigma$ , $S$ , $\Gamma$ , $\delta$ , $\omega$ , $s_0$ ).

$\Sigma$ is the input alphabet (a finite non-empty set of symbols) -> our events;
$S$ is a finite non-empty set of states;
$\Gamma$ is the output alphabet;
$\delta$ is the state-transition function: $\delta: S \times \Sigma \rightarrow S$
$\omega$ is the output-transition function: $\omega: S \rightarrow \Gamma$
$s_0$ is an initial state, an element of $S$ ; and
$\delta \subseteq S \times (\Sigma \cup \{\epsilon\}) \times (\Gamma \cup \{\epsilon\}) \times S$ (where ε is the empty string) is the transition relation.

Given any initial state in $s_0$ , to transition our state to the next state with our output alphabet, our transition would be:

$\delta: s_0 \times \Sigma \rightarrow S$

$\omega: s_0 \rightarrow \Gamma$

Examples of basic Moore machines

Unlike a Mealy machine, we can't coalesce the transition and output functions together as a single transition function. The behavior of the output function is synchronous to the state change. As such, we end up with something like this (in Rescript):

type trafficLightStatus =
  | Red
  | Amber
  | Green
  | FlashingRed

type input =
  | ExpireTime
  | Error
  | Restart

type outputFn = (state) =>
  switch (state) {
  |  Red => (Red, 60.0)
  |  Green => (Green, 60.0)
  |  Amber => (Amber, 60.0)
  |  FlashingRed => (FlashingRed, 30.0)
  }

let transitionFn = (state, input) =>
  switch (state, input) {
  | (Red, ExpireTime) => Green(60.0)
  | (Red, Error) => FlashingRed(30.0)
  | (Green, ExpireTime) => Amber(60.0)
  | (Green, Error) => FlashingRed(30.0)
  | (Amber, ExpireTime) => Red(60.0)
  | (Amber, Error) => FlashingRed(30.0)
  | (FlashingRed, Restart) => Red(60.0)
  | _ => state
  };

let output = outputFn(transitionFn(Red, ExpireTime)) // (Green, 60.0)

Differences between

With formal [[Finite-state transducer]]s

Moore machines are a type of generator and are not used in processing natural language. As such, they do not have a concept of a final state.

With [[Mealy machine]]s

Both Mealy and Moore machines are generator-type state machines and can be used to parse regular language. The outputs on a Mealy machine depend on both the state and inputs, whereas a Moore machine have their outputs synchronously change with the state.

Every Moore machine can be converted to a Mealy machine and every Mealy machine can be converted to a Moore machine. Moore machine and Mealy machine are equivalent.

Properties

Location

Stats