Mealy machine

What is a Mealy machine?

A Mealy machine is a finite-state-automata where the output values are determined by its current state and current inputs. It is the closest definition to a deterministic finite-state-transducer.

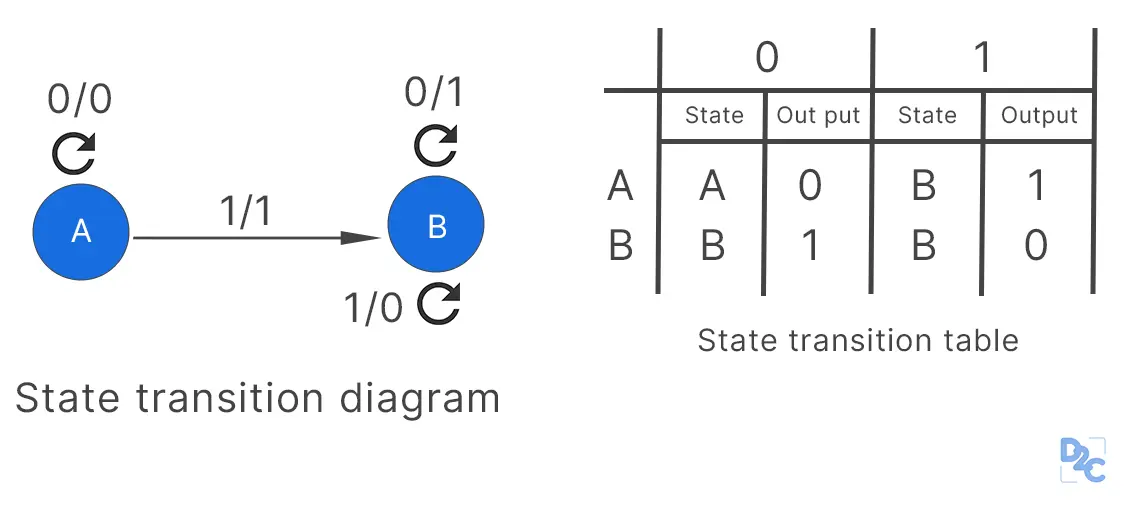
Mathematical model

As per the general classification noted on UC Davis outline on transducers (formatted with similar variables to [[Finite-state automata]]s), a deterministic Mealy machine has 6 main variables associated with its definition (a sextuple): ( $\Sigma$ , $S$ , $\Gamma$ , $\delta$ , $\omega$ , $s_0$ ).

$\Sigma$ is the input alphabet (a finite non-empty set of symbols) -> our events;
$S$ is a finite non-empty set of states;
$\Gamma$ is the output alphabet;
$\delta$ is the state-transition function: $\delta: S \times \Sigma \rightarrow S$
$\omega$ is the output-transition function: $\omega: S \times \Sigma \rightarrow \Gamma$
$s_0$ is an initial state, an element of $S$ ; and
$\delta \subseteq S \times (\Sigma \cup \{\epsilon\}) \times (\Gamma \cup \{\epsilon\}) \times S$ (where ε is the empty string) is the transition relation.

Some formulations also allow transition and output functions to be combined as a single function:

$\delta: S \times \Sigma \rightarrow S \times \Gamma$

Given any initial state in $s_0$ , to transition our state to the next state with our output alphabet, our transition would be:

$\delta: s_0 \times \Sigma \rightarrow S$

$\omega: s_0 \times \Sigma \rightarrow \Gamma$

Examples of basic Mealy machines

Our example from [[Finite-state transducer]]s fits perfectly here as our transition and output function are coalesced as a single function.

// expiry represents our arbitrary output (in seconds)
type expiry = float;

// expiry here is used in a constructor as an arbitrary output
type trafficLightStatus =
  | Red(expiry)
  | Amber(expiry)
  | Green(expiry)
  | FlashingRed(expiry)

// elapsed here is used in a constructor as an arbitrary input
type input =
  | ExpireTime
  | Error
  | Restart

let transition = (state, input) =>
  switch (state, input) {
  | (Red(expiry), ExpireTime) => Green(60.0)
  | (Red(expiry), Error) => FlashingRed(30.0)
  | (Green(expiry), ExpireTime) => Amber(60.0)
  | (Green(expiry), Error) => FlashingRed(30.0)
  | (Amber(expiry), ExpireTime) => Red(60.0)
  | (Amber(expiry), Error) => FlashingRed(30.0)
  | (FlashingRed(expiry), Restart) => Red(60.0)
  | _ => state
  };

Differences between

With formal [[Finite-state transducer]]s

Mealy machines are a type of generator and are not used in processing language. As such, they do not have a concept of a final state.

With [[Moore machine]]s

oth Mealy and Moore machines are generator-type state machines and can be used to parse regular language. The outputs on a Mealy machine depend on both the state and inputs, whereas a Moore machine have their outputs synchronously change with the state.

Every Moore machine can be converted to a Mealy machine and every Mealy machine can be converted to a Moore machine. Moore machine and Mealy machine are equivalent.

Properties

Location

Stats